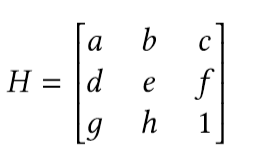The challenge
The power of the computer vision (CV) technology for public safety is redefining the whole landscape of the area. While traditional video monitoring systems have become common to the point of necessity, the usage of artificial intelligence in this area is still considered a novelty.
Apart from object detection, there’s another major task in Public Surveillance systems — object tracking. This task gets more complicated when filming conditions worsen.
It is a relatively common scenario in Public Safety when the video that needs to be analyzed has been shot with a moving camera — for instance, a body-worn camera used by the police. Naturally, it causes several problems with determining the relative position of objects.
Firstly, it’s not exactly clear what made an object shift — the movement of the object itself or camera movement. Secondly, when the scene changes due to camera rotation, different objects can obtain the same coordinates (as seen in the picture below).

Here we’re not talking about the case where an object is constantly in the frame and changes its position gradually (such cases are covered by classic trackers). We’re also not considering the case where the filming conditions are normal or where the camera is stationary.
If the filming conditions are bad and/or the movements are sharp, even the best trackers can fail the task. We detect an object and then lose it (e.g. people turn around and their faces can’t be detected) — which is the exact moment when the camera shifts. It leads to assuming the person we detected before is a new person.
Person identification also doesn’t work if the filming conditions are bad.
We propose a solution to such cases with the EvenVizion component.
Background: Homography
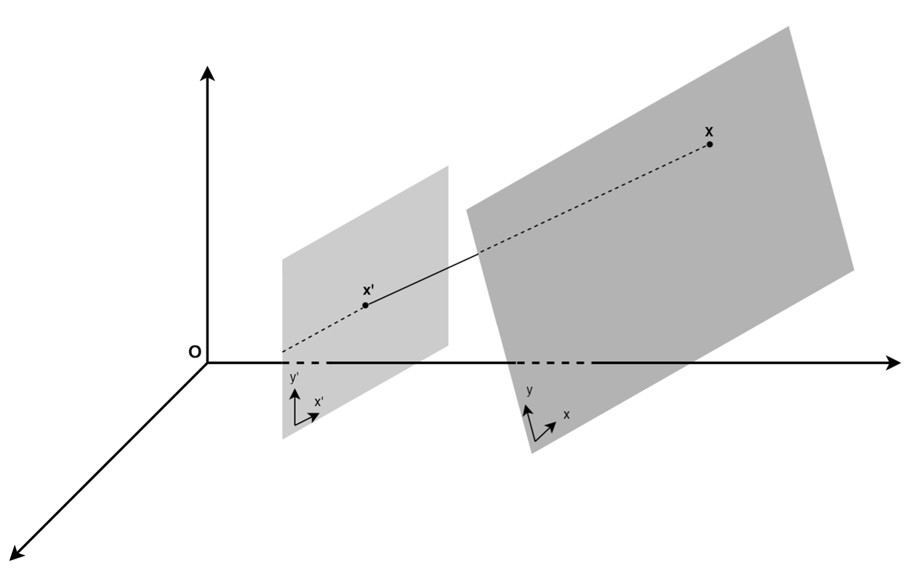
To determine the position of an object, we set the main task — to create a fixed coordinate system. To solve this, it is necessary to find a transformation that will translate all coordinates of the α plane into coordinates relative to the β plane.
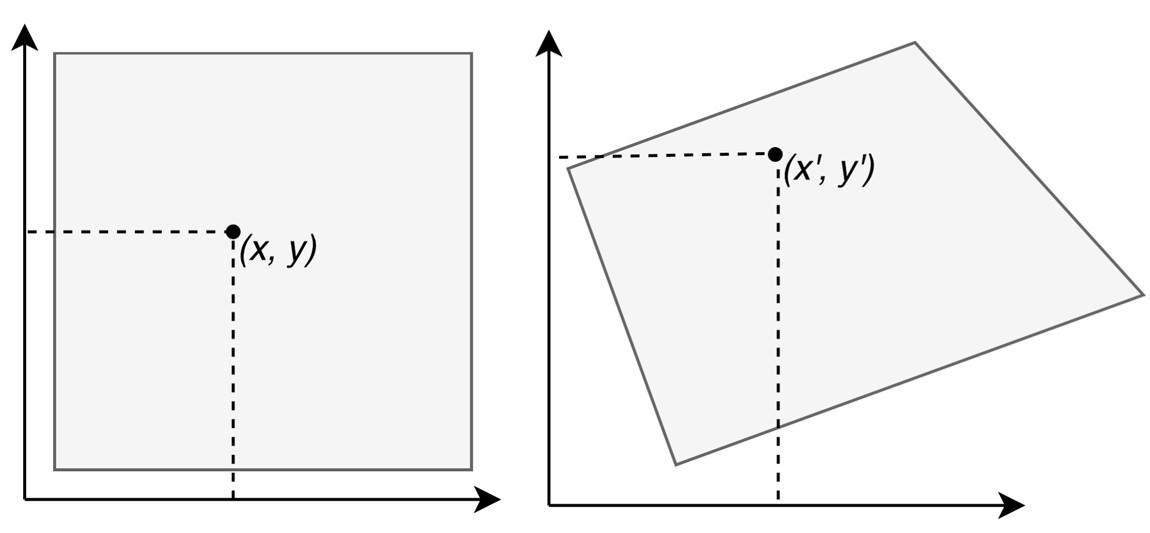
Comparison of two planes
To describe the change in the position of an object in the α plane as compared to the β plane it is possible to use a projective transformation (homography).
Let’s consider the parameters by which this transformation is characterized and how we can obtain new coordinates with its help. The projective transformation is characterized by matrix H:
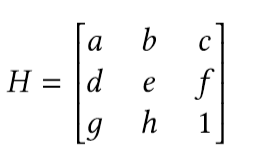
a, e — scaling in x and y respectively
b, d — shift along the axes (affects the rotation together with a and e)
c, f — offset along the axes
g, h — change of the perspective
Using this matrix, we can describe the change in the coordinates of one object between two frames, if this change is caused by camera movement. Then it becomes possible to get new coordinates.
Pipeline
So how do we get to a fixed coordinate system? To resolve this, we identified the following steps:
1. Compare two consecutive frames;
2. Find a transformation that will translate object coordinates on the current frame into the coordinates relative to the point (0,0), while being projective:
Projective transformation
Now we consider that there is a set of common points for two frames and their original coordinates, which are relative to the frame.
An example of camera movement that caused object scaling:
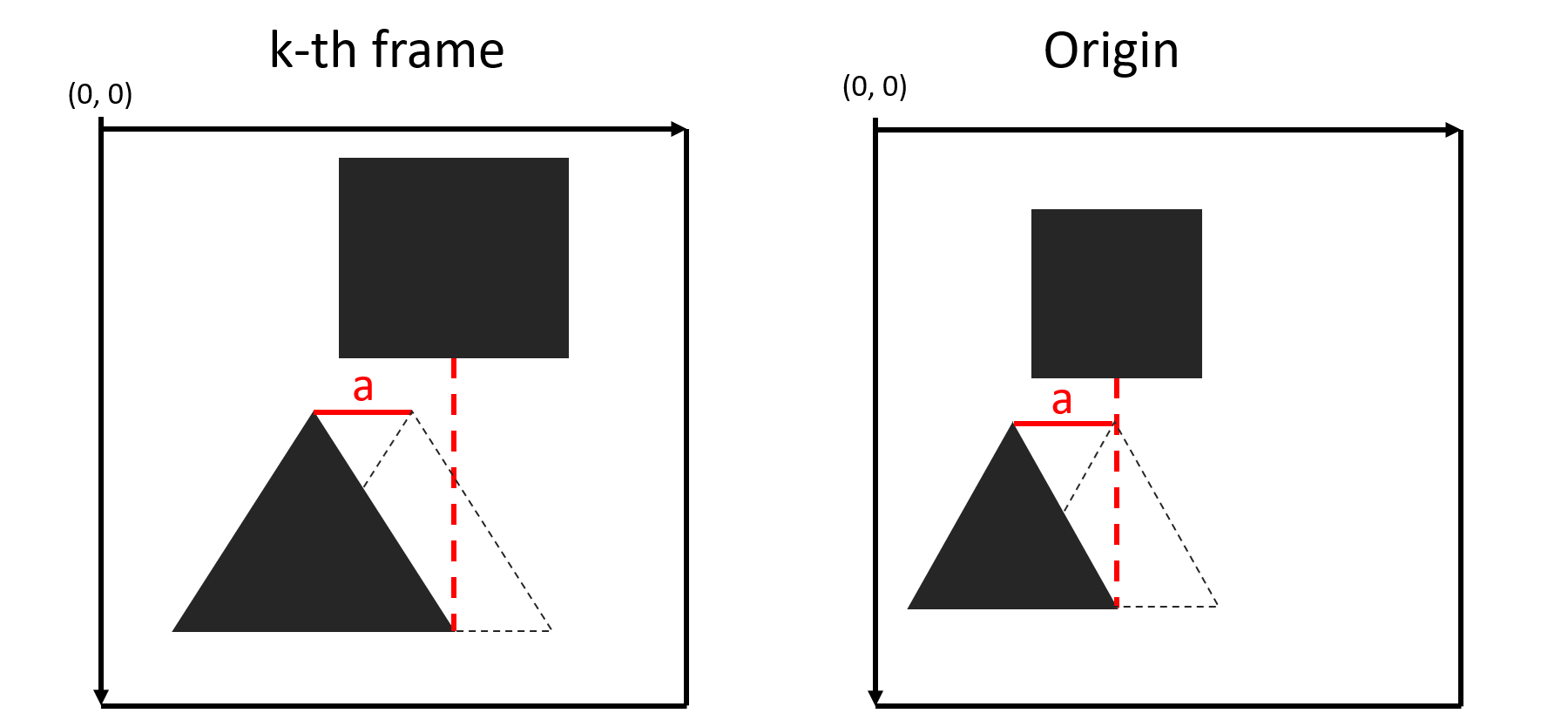
Here is an example of a camera movement in which objects are scaled. When searching for a transformation between two frames, we need to consider all the transformations that have occurred since the first frame.
We can describe the movement of the camera between all the previous pairs of consecutive frames using the homography matrices. As a result, we will receive a transformation that will translate the coordinates of the object on the current frame into the coordinates relative to the origin (0,0).
How we match special points
The main idea of the whole pipeline is to calculate the homography matrix using matching points. The approaches to finding such points can be different.
By special point here we mean the point of an object that will be found on another image of the same object with a high degree of probability. The correspondence between singular points is established using their descriptors.
We used SIFT (Scale-invariant feature transform), SURF (Speeded Up Robust Features) and ORB (Oriented FAST and Rotated BRIEF) to find special points and their descriptors. Three types of points were used to ensure they cover the maximum possible area of the frame.
The result is the following matching points highlighting scheme:
1. Special points and their descriptors are highlighted on the images.
2. By the coincidence of descriptors, special points that correspond to each other (the matching points mentioned above) are allocated.
For each descriptor, we look at the two best matches using the k-nearest neighbor algorithm. Then we run Lowe’s ratio test to remove false positives. Thus, for each point of the k-1st frame, we obtain the corresponding point on the k-th. Using the obtained matching points, we connect the two frames.
When we use these algorithms to find matching points, a problem arises: some points can cling to an object. The movement of such points depends not only on the movement of the camera (static object), but also on the movement of the object itself — a person, a car etc. Therefore, it is necessary to filter these points out.
We developed the following filtering option:
- we get “dirty” matching points with coordinates that include points on moving objects
- we find the homography matrix that will translate the coordinates of the k-th frame into the plane of the k-1 frame
- we apply it to the discovered points and obtain their new coordinates
- finally, we apply filtration of the points
The only points left are those on stationary objects. We use them particularly when calculating the homography matrix.
About the EvenVizion component
We created the component that allows defining the relative position of objects and to translate the coordinates of an object relative to the frame into a fixed coordinate system. As the main point of this solution was to evaluate plane transformation using key points, we demonstrated that the task can be solved even in bad filming conditions (sharp camera movement, bad weather conditions, filming in the dark and so on).
After running the EvenVizion component script, we get 3 visualizations.
1. Matching points visualization:

2. Heatmap visualization:

3. Fixed coordinate system visualization:

As a result, we get a final stabilized video looking like this:
Conclusion
With the introduction of CV-based analysis, the Video Monitoring Systems environment has been changing over the past several years. Oxagile leverages proven expertise in CV-based Public Safety solutions and managed services to tackle increasingly demanding business cases. The EvenVizion component has been developed to address one of such challenges.
The tasks of object detection and tracking set for video monitoring systems can be unsolvable by traditional means. In the case when the camera is moving even the best trackers can fail.
That’s why we created the component that helps to localize the camera and stabilize footage for future analysis using CV-based methods.
We at Oxagile R&D hope that our contribution to the open source society will be of value for researchers who face the problem of shaky camera footage. This is only the beginning of our Github journey.